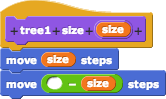
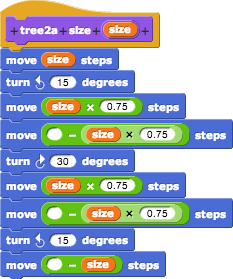
4. That tree2a block is pretty long and repetitive. But we can simplify it if we notice that in two places it has a move forward/move back pair of blocks, and that this is what tree1 does! So we can use tree1 to shorten tree2. Compare the code below to convince yourself that the new tree2 will work the same as the original tree2a.

tree1	tree2a (old version)	tree2 (new version)

Note that the tree blocks inside this tree2 script are tree1 blocks, not tree2 blocks! So there's no mysterious tree-using-tree situation (yet)! It's not unusual for one already-written block (also known as a helper block or a helper function) to be used in another block's script.

5. Make a tree3 block that uses the tree2 block, on the same pattern. Don't forget about the "duplicate" feature in Snap!, which will save you a bunch of time making tree3. Once you're done, try out tree3 and you should see output that looks something like the following:

6. If you can stand it, make a tree4 block that uses the tree3 block and try it out.

This would be a good time to save your project if you haven't already.

7. These blocks all look exactly the same, don't they? So it makes sense to wonder if we can replace them all with a single tree block. Here's the big idea: We can write a tree block that uses itself in its own script provided that it knows how many levels it's expected to draw! So, in addition to the size input, it'll have a levels input:

In the earlier steps, tree3 used tree2; tree2 used tree1. If you actually had the patience to work up to a tree437 block, what block would it call for its two branches? To generalize the pattern, tree will use tree, but reducing the number of levels by 1:

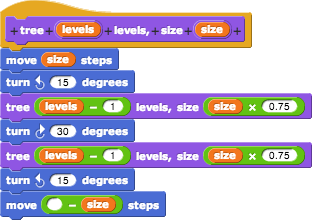
For example, given a levels input of 5, tree will call two trees with a levels input of 4. Those two trees in turn will each call two more trees with a levels input of 3. This pattern continues on and on, with the levels and size inputs getting smaller and smaller. Ideally, we want the levels input to eventually reach and finish at 1, signifying our most basic tree.

Now try running the tree block. What happens? Why does it happen? When you know the answer, go to the next activity.
Hint: Try to follow the tree block for a small levels input such as 3, and keep track of the decreasing levels input as you call more trees. What happens for level 1 (our most basic tree)?