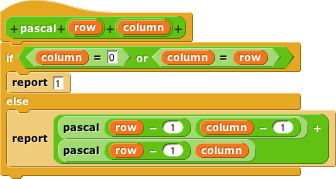
Here's our solution:

If the desired position is at the left (column=0) or the right (column=row) end of a row, then the value is 1. That's the base case. In the recursive case, the desired value is the sum of two values in the previous row (the two recursive calls).

This is like the other examples we've seen in that what's reported is the result from a combiner block, in this case +. But it's different in that the two things being combined are both recursive calls.

Just how many recursive calls are needed to compute a value in Pascal's Triangle? In, let's say, the middle of row 10? (Values near an end of a row are faster to compute because they reach a base case quickly.)

☞ How many seconds does it take to compute pascal(10, 5)? How about pascal(12, 6)? What's your guess about how long it would take to compute pascal(20,10)?

As a first approximation, pretend that the computation would never reach a base case until row 0. Then a value in row 10 will make two recursive calls into row 9. Each of those will make two recursive calls, for a total of four into row 8. Each of those makes two recursive calls, so there are eight calls into row 7, 16 into row 6, 32 into row 5, 64 into row 4, 128 into row 3, 256 into row 2, 512 into row 1, and 1024 into row 0! In reality the situation isn't quite so bad, because by row 5 you're already hitting the ends of the row. But still, roughly speaking, it takes something like 2ⁿ recursive calls to find a value near the middle of row n of the triangle.

☞ Make a global variable called count and set it to 0. Modify your pascal script to keep count of recursive calls:

How many calls are actually made when you compute pascal(10, 5)? pascal(12, 6)? (Don't forget to reset count to 0 for each experiment.) Make a guess for pascal(14, 7) and see how close you come.

If all those recursive calls were really contributing new information to the result, then the slowness of this algorithm would be unfortunate but unavoidable. In fact, though, a lot of them are redundant. Consider these calls:

There are two calls to pascal(8, 4), out of four calls on row 8 altogether. The redundancy just gets worse in higher rows. In fact, the total number of numbers at or above row 10 is smaller than 10², and in general n² at or above row n.

☞ Why?

☞ For row 20, estimate 2²⁰ (the number of calls made) and 20² (the number of unique values needed).

☞ Optional Exercise: Figure out how to modify the pascal script to get an exact count of the number of unique row – column input pairs used in a computation.

☞ Optional Exercise: Use a list structure to keep track of already-computed values, and when the same inputs are given again, look up the saved value instead of making more recursive calls. If you do not remember what this technique is called, ask your partner or a member of course staff.

Some of you might remember from an earlier exposure to Pascal's Triangle that there's a formula to compute the numbers in the table:

This can be computed, without using recursion at all, in a time proportional to the row number n. The moral: An ounce of math is worth a pound of computer science... sometimes.