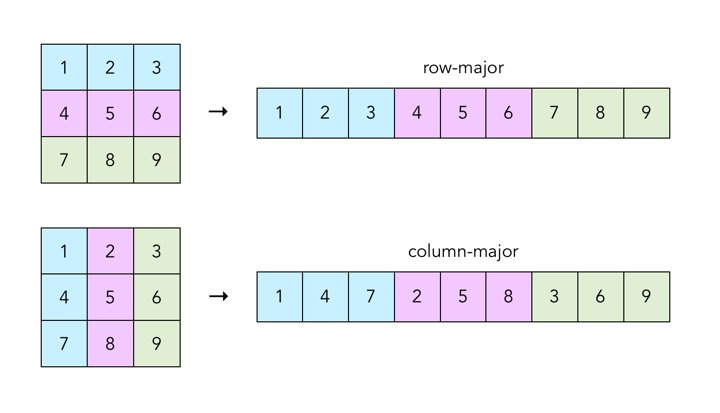
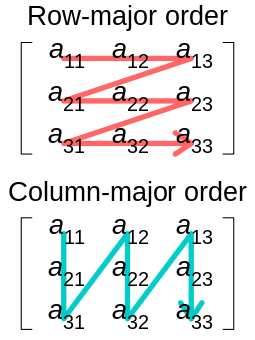
Row-major order and column-major order are methods used for storing multi-dimensional arrays in linear, one-dimensional memory spaces like RAM. The choice between row-major order and column-major order can impact performance depending on the nature of the operations being performed on the array. Here are some considerations and reasons for using row-major order:

• In some programming languages like C and C++, arrays are stored in row-major order by default. Sticking with the default can make code more straightforward and easier to understand, especially for others who might be reading or maintaining your code.
• Modern processors use caches to reduce the average time to access memory. When data is accessed in memory, nearby data is often also loaded into cache in anticipation of future accesses. Because of this, accessing elements that are nearby in memory (such as elements within the same row of a row-major order array) can be much faster than accessing elements that are farther away in memory (such as elements in different rows). If your algorithms access array elements in a row-by-row manner, then using row-major order can significantly improve cache performance and overall speed.

The way we represent a 2D board is through a list of lists. For example:
has 3 rows and 3 columns.

We want to flatten a 2D list into a 1D array in two different ways: row-major order (rmo) and column-major order (cmo). For both blocks, recursion is banned. You must use either HOFs or Iteration in your solution.


TODO: Implement the RMO of board block. The input is a 2D board of size NxN (N rows, N columns). The output is a 1D list in row-major order. the first N items of the list will be the entries in row 1. The next N items will be the entries in row 2, and so on.