Using the framework provided, implement a Snap! block in the Unsorted sprite that finds a number in a list of unsorted numbers using the strategy that we discussed. The block should accept the target number (the "needle") and a full list of numbers (the "haystack") as arguments, and return the index of the number's position in the list. What was the strategy we discussed for unsorted lists, and how could you implement it? Two empty blocks are provided for you, one for unsorted and the other for sorted lists. Fill in the implementation for each block. Using the framework, determine how their running time changes as the list size increases. Which is faster for a list of size 5? 50? 500? 5000? Why do you think this is?


Searching Unsorted Data

Find Number In Unsorted List

Unsorted data doesn't give you a lot to work with. Your knowledge is limited to strictly the most obvious information: the numbers themselves. This makes strategy somewhat non-existent; the best you can do, on average, is to simply start at the beginning and search through the list one by one. This approach can become incredibly slow if we're dealing with a lot of data, but is actually fairly quick when working with smaller amounts of data. In addition, the block is relatively straightforward to create and doesn't require the data to be put into a particular order to work. The block should return the location of the number in the list, or -1 if the number doesn't exist in the list.

Searching Sorted Data

Find Number In Sorted List
Searching for Numbers
You could say that putting information in a particular order (lowest to highest, for example) actually creates new information. Instead of being a simple list of numbers, sorting the information adds order and allows us to make additional assumptions that we weren't able to make before. This type of information is different from the numbers themselves: it is not stored in a variable or list, but becomes a property of the information itself. We can use the property to reduce the number of checks we have to do to find a particular number. However, the list must be sorted before we can make use of the order.

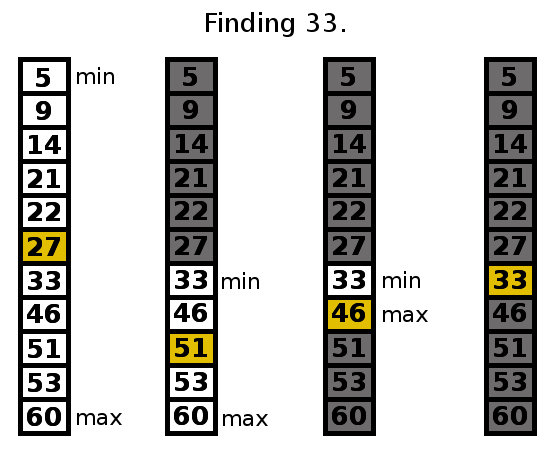
Searching through sorted data, while faster, also requires a more complicated block. We won't need to search through every space in the list anymore -- we can assume that many of them won't work. We can keep track of the range of numbers in a list that are a possible solution to the problem (see diagram) by recording the minimum and maximum slots that could possibly contain our number. This range should shrink after each guess because you can throw away the half of the numbers on the wrong side of the center point. Here's how things should generally work:
  1. The range of possibilities starts off including every number in the list (the minimum is position #1 and the maximum is the final position). Let's say that we're searching for the number 33 as shown in the diagram. Start your search around the middle of the list. Check the value of the number there.
  2. If the number at the spot you searched is greater than 33, set the maximum to the slot before the one you just searched (after all, 33 CAN'T be on the larger side if it's is smaller than the one you just checked!). If the number is smaller than 33, set the minimum to the slot after the one you searched.
  3. Check the middle position of your new range. Repeat step 2 for this new range and reduce the range further.
  4. Continue to repeat steps 2 & 3 until either (a) you find the number you're looking for or (b) you get in a position where the minimum is greater than the maximum (try to work out an example where this happens). If (b) happens, it means that the number doesn't exist in the list. In this case report -1.

Flying Even Higher

Let’s say this application is going to be used to find many numbers every time it is launched -- possibly the same number multiple times. How could we speed this process up even more?