In computer science, one thing we love to do is to take specific problems and generalize them. What was specific in ? Each had exactly two paths out of it (if it wasn't a dead-end), but that's not very realistic. Most places have many paths out of them.

Fortunately, the problem statement won't change much. All we do is replace and with , which returns a list of neighbor places, each reached by going down a particular path out of that place. For example, using the same graph as before (reprinted for your convenience):

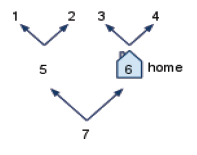
• go-neighbors(5) ==> (1 2)
• go-neighbors(6) ==> (3 4)
• go-neighbors(7) ==> (5 6)

... but you could imagine that some forests might have only one path out of a place, or even a hundred! Like before, calling is an error if is a dead-end, so will never return a list with no elements.

Write the block that can handle the generalized forests described above. You will need to use HOFs in your solution, but it will not require drastic changes from your original block.